termoelettricità

termoelettricità In fisica, genericamente l’insieme dei fenomeni elettrici collegati a fenomeni termici: quindi, non soltanto gli effetti termoelettrici propriamente detti, e cioè gli effetti Seebeck, Peltier, Thomson, consistenti in fenomeni di correlazione tra forze elettromotrici e differenze di temperatura in materiali conduttori, ma anche, per es., l’effetto Joule, fenomeno di correlazione fra quantità di elettricità e quantità di calore in gioco in un conduttore percorso da corrente. Il termine è peraltro correntemente usato, con significato specifico, per indicare gli effetti termoelettrici citati e anche la parte della fisica che si occupa di tali effetti.

Effetto Seebeck in conduttori metallici

fig. 1

fig. 2

fig. 3

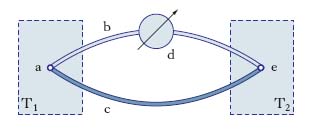
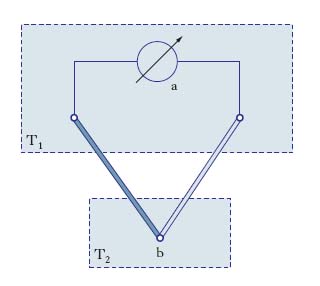
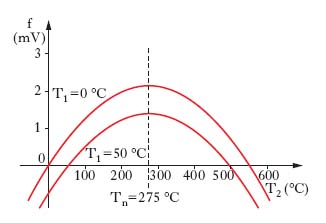
Scoperto da T.J. Seebeck nel 1821, consiste nel fatto che se le giunzioni (fig. 1) di un circuito costituito da due conduttori metallici, o anche da due semiconduttori diversi (quali le giunzioni a ed e di b e c; fig. 1), in serie fra loro, sono a temperature T₁, T₂ diverse, nella coppia insorge una forza elettromotrice (f.e.m.), la forza elettromotrice termoelettrica di Seebeck o forza termoe;lettromotrice: un galvanometro d inseri;to in uno dei conduttori segnala il passaggio di una corrente elettrica (corrente termoelettrica), che permane sinché esiste differenza di temperatura fra le due giunzioni (perché l’inserzione del galvanometro non perturbi il fenomeno, i contatti galvanometro-coppia devono trovarsi alla stessa temperatura). Una disposizione particolarmente comoda per le misurazioni è quella schematizzata nella fig. 2, detta anche coppia, o pinza, termoelettrica: il voltmetro, a, è inserito in una delle giunzioni e, se di resistenza interna sufficientemente alta, indica direttamente il valore della forza elettromotrice che si manifesta quando la temperatura T₂ dell’altra giunzione della coppia, b, è diversa da quella T₁, a cui si trovano le estremità dei due conduttori della coppia e il voltmetro (di norma, la temperatura ambiente). Se si tiene costante T₁ e si fa variare T_2, si trova per la f.e.m., f, un andamento sul tipo di quello schematizzato nella fig. 3 per la coppia Fe-Cu con una temperatura di riferimento T₁ pari a 0 °C. Come si vede, f è sempre piuttosto piccola (al massimo è dell’ordine di qualche millivolt) e per T₁<T₂ è positiva, vale a dire che il ferro è a potenziale maggiore del rame, sinché T₂ è minore di 550 °C, superato il quale valore, detto temperatura, o punto, d’inversione, diventa negativa. È importante la circostanza che f dipende soltanto dalla natura dei conduttori a contatto e dalle temperature delle giunzioni, ma non dalla forma e dall’estensione di queste ultime. La quantità, variabile al variare di T₂, a_T=df/dT, misurata dal coefficiente angolare della tangente alla curva f(T), ha il nome di potere termoelettrico della coppia considerata (alla temperatura considerata). Se si passa a un altro valore per la temperatura di riferimento, T₁, il diagramma che si ottiene è quello precedente, traslato però parallelamente all’asse delle forze elettromotrici in modo che sia f=0 per T₂ pari al nuovo valore di T₁ (in fig. 3, si passa per T₁ da 0 a 50 °C); così cambiano, ovviamente, i valori di f corrispondenti ai vari valori di T₂ e cambia anche il punto d’inversione, ma non cambia il valore T_n della temperatura in corrispondenza al quale f raggiunge il suo valore massimo. Tale temperatura, che è dunque una caratteristica intrinseca della coppia considerata, ha il nome di temperatura neutra, o punto neutro, in quanto per essa il potere termoelettrico è, naturalmente, nullo. I diagrammi f(T₂) che l’esperienza fornisce per vari valori di T₁ hanno, con ottima approssimazione, andamento parabolico; indicando con A, B i due metalli costituenti una generica coppia, si può scrivere:

T₂+T₁

f_AB,T1,T2=β_AB(T₂−T₁)(T_nAB− −−−−−−−).

1

Tale relazione è l’equazione di una famiglia di parabole nel piano (T₂, f), omofocali, con asse T₂=T_n e parametro T₁; in essa compaiono come costanti caratteristiche della coppia A-B il punto neutro T_nAB e la quantità β_AB. Quest’ultima è legata al potere termoelettrico dalla relazione: a_T=β(T_n−T₂); così, il potere termoelettrico dipende linearmente dalla temperatura, annullandosi al punto neutro. È da osservare che se è β_AB>0, si usa dire che il metallo A è termoelettricamente positivo rispetto al metallo B (e questo è termoelettricamente negativo rispetto ad A): per T₂ compresa fra T₁ e il punto d’inversione 2T_n−T₁, la forza elettromotrice risulta positiva, cioè A si trova a potenziale maggiore di B.

Effetto Peltier in conduttori metallici

Scoperto da J.-C.-A. Peltier nel 1834, consiste nel fatto che, se in un circuito costituito da due conduttori metallici (o anche semiconduttori) diversi, sul tipo di quello della fig. 1, si fa circolare una corrente elettrica, inserendo un generatore di forza elettromotrice, una delle giunzioni si riscalda, mentre l’altra si raffredda; se si inverte il verso della corrente, la giunzione che prima si riscaldava si raffredda, e viceversa. Nel passato era usuale, a causa degli aspetti formali del fenomeno, parlare di effetto termoelettrico inverso, considerando effetto termoelettrico diretto l’effetto Seebeck; tale uso non è però corretto, in quanto tra i due effetti non vi è una relazione di inversione, ma di dipendenza. Se si misura la quantità di calore Q ceduta o assorbita da una giunzione, si trova che è Q=π_AB,TiΔt, essendo i l’intensità della corrente, Δt l’intervallo di tempo in cui la corrente scorre, π_AB,T una grandezza caratteristica della coppia in esame, dipendente soltanto dalla natura dei due conduttori A, B e dalla temperatura della giunzione, ma non dalla forma e dall’estensione di quest’ultima: essa è detta coefficiente di Peltier o anche forza elettromotrice di Peltier. Convenendo di assumere positiva la quantità di calore emessa dalla giunzione che si riscalda e positiva l’intensità della corrente che scorre, nella giunzione, dal conduttore A verso il conduttore B, risulta che π_AB,T è positiva se la giunzione cede calore all’ambiente quando la corrente scorre da A a B. Per l’accennata invertibilità dell’effetto, è π_AB,T=−π_BA,T. Alcuni valori, a temperatura di 0 °C sono: π_Bi–Cu=21 mV, π_Fe–Cu=2,8 mV, π_Cu–Zn=0,03 mV. La misurazione di queste piccole quantità è piuttosto delicata, e, inoltre, allo sviluppo di calore per effetto Peltier si sovrappone lo sviluppo di calore per effetto Joule. La procedura di misurazione tipica, che mette a profitto la dipendenza dell’effetto Peltier dall’intensità della corrente e quella dell’effetto Joule dal quadrato di tale intensità, consiste nel misurare la quantità di calore in gioco a una giunzione dapprima con la corrente in un verso, per es. da A a B (Q_AB), e poi con la corrente nel verso opposto (Q_BA), sempre con la medesima intensità i e per lo stesso intervallo di tempo Δt; si ha Q_AB=(π_ABi+Ri²)Δt, Q_BA=(−π_ABi+Ri²)Δt, con R resistenza della giunzione, da cui: Q_AB−Q_BA=2π_ABiΔt. Per avere misure sufficientemente precise occorre che il termine di effetto Joule, Ri², sia piccolo rispetto all’altro, e ciò si ottiene operando con giunzioni a bassa resistenza, cioè con giunzioni estese e fra conduttori di grossa sezione.

Effetto Thomson

fig. 4

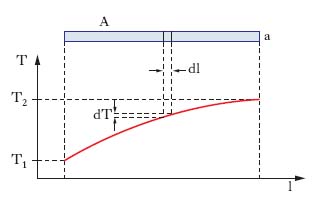
Scoperto da W. Thomson (lord Kelvin) nel 1854, consiste nell’insorgere di una forza elettromotrice (forza elettromotrice di Thomson) in un conduttore metallico (o anche in un semiconduttore) omogeneo a (fig. 4) in cui sia mantenuto un gradiente di temperatura. L’esperienza mostra che tale forza elettromotrice, ϕ, è tanto maggiore quanto maggiore è la differenza di temperatura T₂−T₁ fra le estremità del conduttore, e non dipende dalla forma e dall’estensione del conduttore né dal modo con cui la temperatura varia lungo il conduttore medesimo (legge dell’indipendenza dal gradiente termico). Considerando un trattino dl di conduttore, lungo il quale la temperatura vari di dT, la forza elettromotrice agli estremi di esso vale d ϕ =τ_A,TdT, avendo τ_A,T, dipendente dalla natura del conduttore in esame, A, e dalla temperatura, il nome di coefficiente di Thomson; per la forza elettromotrice complessiva, si ha:

ϕ_A,T2,T1= ∫^T2_T1 τ_A,T dT.

Alcuni valori di τ, in μV/K, a temperatura ordinaria sono: τ_Cu=+2, τ_Fe= −8, τ_Pt=+13; per la costantana, è τ=−25 μV/K. A valori positivi di τ corrisponde il fatto che il campo elettromotore è diretto come il gradiente di temperatura, cioè che nel conduttore vi è una migrazione di cariche negative verso l’estremità a temperatura minore. A causa del loro piccolo valore, confrontabile con quello delle forze elettromotrici dovute al rumore termico, la misurazione diretta delle forze elettromotrici di Thomson è piuttosto difficoltosa; normalmente si ricorre a una misurazione indiretta, basata sul fatto che se il conduttore è percorso da corrente, accanto a sviluppo di calore per effetto Joule vi è da considerare uno scambio di calore con l’ambiente, il cui verso dipende dal verso della corrente e dall’essere le varie zone più o meno calde: il calore messo così in gioco, detto calore di Thomson, corrisponde all’energia del campo elettromotore di Thomson. Precisamente, per il trattino dl di conduttore la quantità di calore vale dQ=τΔTiΔt, essendo i l’intensità della corrente e Δt l’intervallo di tempo in cui passa corrente; quest’ultima è assunta positiva se scorre nel verso delle temperature crescenti.

Teoria della termoelettricità

Gli effetti descritti trovano spiegazione in fenomeni di diffusione termica dei portatori di carica (elettroni e lacune) nei conduttori e in fenomeni di contatto alle giunzioni fra conduttori di natura diversa; poiché la diffusione provoca l’effetto Thomson e i fenomeni alle giunzioni sono alla base dell’effetto Peltier, questi due effetti sono da considerarsi principali e indipendenti, mentre l’effetto Seebeck, benché scoperto per primo e considerato l’effetto termoelettrico per eccellenza, è in realtà un fenomeno derivante dagli altri due. Relativamente all’effetto Thomson, la spiegazione, in termini qualitativi, sta nel fatto che i portatori di carica, diffondendo in seno al conduttore, vengono ad avere una densità minore nelle zone a temperatura maggiore; quindi, se le cariche in questione sono elettroni, si porta a potenziale maggiore l’estremo più caldo (coefficiente di Thomson positivo), mentre se sono lacune è l’estremo più freddo a essere a potenziale maggiore (coefficiente di Thomson negativo). In termini quantitativi, tutto dipende dal fatto che l’energia di Fermi per i portatori di carica nel conduttore è una funzione leggermente decrescente della temperatura. Pertanto, in un conduttore omogeneo non isotermo il livello di Fermi non è ovunque esattamente lo stesso, ma segue leggermente l’andamento della temperatura, e ciò comporta l’insorgere di piccole forze elettromotrici, quelle di Thomson. Quanto all’effetto Peltier, si deve tener presente che l’effetto Volta a ogni giunzione bimetallica, o l’analogo effetto che si manifesta quando la giunzione è costituita da almeno un semiconduttore, porta allo stabilirsi di un unico livello di Fermi, e quindi di un’unica energia totale dei portatori di carica, in tutta la giunzione, in virtù di una variazione della sola energia potenziale per l’insorgere di una conveniente differenza di potenziale di contatto; le energie cinetiche dei portatori di carica sono quindi necessariamente diverse da una parte e dall’altra della giunzione e quando, facendo scorrere una corrente, si forzano i portatori a superare la giunzione, l’eccesso o il difetto di energia cinetica dei portatori che transitano si traduce in liberazione o assorbimento di energia termica nella giunzione. L’accennata dipendenza dell’effetto Seebeck dagli altri due si spiega tenendo conto del fatto che è diversa la situazione di giunzioni a temperatura diversa, cioè tenendo conto del fatto che gli effetti Volta alle due giunzioni di una coppia bimetallica non isoterma (e analogamente in presenza di almeno un semiconduttore) non si compensano più, come invece accade quando tutto il sistema è isotermo.