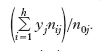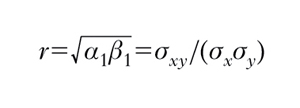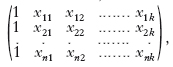regressione

Geologia

Lo spostamento verso il mare della linea di costa. Questo fenomeno (opposto a quello della trasgressione) può verificarsi durante condizioni di stazionarietà o di sollevamento relativo del livello marino, se vi è un eccesso di apporto sedimentario; in questi casi la r. è definita deposizionale ed è anche chiamata progradazione. Se invece la r. avviene a causa di un abbassamento relativo del livello marino che provoca bruschi spostamenti della linea di costa verso il mare, associati a estesi fenomeni di erosione subaerea, è definita r. erosiva.

Linguistica

Figura retorica, detta anche epanodo (➔).

Psicologia

In psichiatria, l’orientamento o la strutturazione dei processi psichici secondo schemi funzionali propri di un’attività meno differenziata di quella normale. La legge di r. (o legge di reversione di T. Ribot) è l’ordine secondo cui nell’indebolimento generale della memoria si perdono i ricordi, che è inverso a quello della loro acquisizione: scompaiono dapprima quelli recenti e poi quelli più antichi.

In psicanalisi, ritorno a stadi precedenti rispetto all’oggetto, allo sviluppo della libido o a quello dell’io. Il concetto di r. è stato inizialmente proposto da S. Freud nell’interpretazione dei sogni, in un triplice senso: r. topica, nel senso dello schema dell’apparato psichico (conscio, preconscio, inconscio); r. temporale, nel senso di un ritorno a formazioni psichiche più antiche; r. formale, nel senso che modi di espressione più arcaici vengono sostituiti a quelli abituali.

Statistica

R. filiale Legge dell’eredità stabilita da F. Galton, secondo cui i figli tenderebbero a variare nello stesso senso dei genitori, ma con intensità minore: i figli di coppie la cui statura sia superiore al valore medio della popolazione sono anch’essi più alti ma il loro scarto medio dalla media è minore di quello dei genitori; i figli tendono dunque a regredire verso la media.

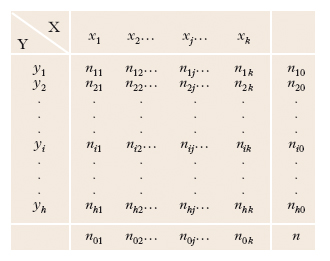
La teoria della r., che prese le mosse dagli studi di Galton sull’ereditarietà, fornisce il metodo per analizzare l’influenza che una o più variabili esercitano su altre. Per illustrare i concetti fondamentali della teoria della r. è sufficiente riferirsi al caso più semplice: quello di un collettivo di n unità statistiche classificate secondo le modalità di due caratteri quantitativi Y, X (per es., peso e statura, oppure età e reddito individuale). Siano y_i e x_j le modalità rispettivamente di Y e X (i = 1, 2, …, h; j = 1, 2, …, k), n_ij il numero delle unità in cui si osservano insieme le modalità y_i e x_j, e n_i0 = n_i1+ … +n_ik, n_0j = n_1j+ … + n_hj il numero complessivo delle unità in cui si osservano rispettivamente le modalità y_i e x_j. I dati possono essere scritti nella seguente tabella a doppia entrata (tabella di correlazione):

Per ogni j è individuata una distribuzione parziale del carattere Y, comprendente n_0j unità, di cui n_1j uguali a y₁, n_2j uguali a y₂, e così via. Si indichi con ȳ_j la media aritmetica di tale distribuzione, pari a

Graficamente, se si riporta una distribuzione doppia in un piano cartesiano, si ottiene una nuvola di punti. L’insieme dei punti (x_i, ȳ_i) viene denominato linea di r.; tale linea può essere interpolata con una retta di equazione y=β₀+β₁x. Seguendo il metodo dei minimi quadrati, si determinano i parametri β₀ e β₁ in modo da minimizzare la quantità

Si dimostra facilmente che ciò equivale a minimizzare la quantità

In altri termini, se si applica il metodo dei minimi quadrati, la retta che interpola la linea di r. è la stessa che interpola tutta la distribuzione. Annullando le derivate parziali della funzione minimanda rispetto a β₀ e β₁ si trova β₁=σ_xy/σ²_x, β₀=ȳ−β₁x̄, dove x̄ e ȳ sono le medie aritmetiche delle distribuzioni marginali di X e Y:

Come risulta dall’espressione dei parametri β₀ e β₁, la retta di r. passa per il punto (x̄, ȳ). Si verifica inoltre facilmente che la somma dei ‘residui’ y_j−β₀−β₁x_j (ossia delle differenze fra i valori effettivamente osservati e quelli teorici costituiti dalle ordinate della retta di r. nei punti di ascissa x_j) moltiplicati per le corrispondenti frequenze n_ij è nulla. Mentre β₀ dipende dalla scelta dell’origine e si annulla per effetto di una traslazione che porti l’origine nel punto (x, ȳ), β₁, che viene denominato coefficiente di r. di Y su X, è indipendente dall’origine, ma varia al variare delle unità di misura. Il coefficiente di r. è la tangente trigonometrica dell’angolo che la retta di r. forma col verso positivo dell’asse X e indica pertanto di quanto vari approssimativamente in media Y quando X subisce un incremento unitario. L’approssimazione, naturalmente, è tanto migliore quanto più la linea di r. si avvicina a una retta. Quando β₁ = 0, le variabili X e Y si dicono incorrelate. Variabili che sono indipendenti sono anche incorrelate, ma non è vero il viceversa. Vi sono perfino casi di dipendenza funzionale con coefficiente di r. nullo: un esempio semplice è y = x², con X distribuita simmetricamente intorno allo zero.

I concetti esposti si estendono facilmente a variabili continue e al caso di più variabili. Quando l’approssimazione fornita dalla retta di r. non è soddisfacente, conviene interpolare la linea di r. con polinomi di grado superiore o con altre funzioni di r., i cui parametri vengono sempre determinati, quando possibile, con il metodo dei minimi quadrati. Accanto alla retta di r. di Y su X può essere considerata quella di X su Y, di equazione:

La media geometrica dei due coefficienti di r. presa col loro segno comune è il coefficiente di correlazione r di Bravais-Pearson:

L’analisi della regressione consiste nella trattazione di un modello probabilistico del tipo:

(i = 1, 2, …, n), dove y_i sono determinazioni campionarie della variabile dipendente Y, x_ij (j = 1, 2, …, k) sono i valori noti, assunti in concomitanza dalle variabili X_j, valori che generalmente vengono trattati come costanti, β_j (j = 0, 1, …, k) sono i parametri o coefficienti di r., di valore incognito e le ε_i rappresentano gli errori di osservazione, che in generale si postulano indipendenti e distribuiti secondo la legge normale con media nulla e varianza σ², che è del pari incognita. In forma matriciale si può scrivere più sinteticamente: y = xβ+ε, dove y è il vettore che ha per componenti y₁, y₂, …, y_n, ossia le osservazioni della variabile Y, x è la matrice

mentre β ed ε sono i vettori di componenti β₀, β₁, …, β_k e, rispettivamente, ε₀, ε₁, …, ε_k. Le stime βˆ₀, βˆ₁, …, βˆ_k dei parametri β₀, β₁, …, β_k, ottenute col metodo dei minimi quadrati che impone di minimizzare la forma quadratica (y−X βˆ)^T (y−X βˆ), sono date, se la matrice X^TX è regolare, da βˆ = (X^TX)^–1 X^Ty, dove βˆ è il vettore di componenti βˆ₀, βˆ₁, …, βˆ_k, e T indica la matrice trasposta. Date le ipotesi fatte, βˆ è un vettore di variabili casuali, distribuite normalmente con medie uguali a β e con la matrice delle varianze e covarianze uguale a σ² (X^TX)^–1. La costante incognita σ², a sua volta, può essere stimata correttamente mediante la quantità

La variabile (n−k−1)/s² è distribuita secondo la legge del χ² con (n−k−1) gradi di libertà ed è indipendente dalle variabili βˆ. Fondandosi su queste proprietà, l’analisi della r. si propone di pervenire a induzioni riguardanti i veri valori dei parametri βˆ, mediante intervalli di confidenza e test di significatività.