Tolomèo, Claudio
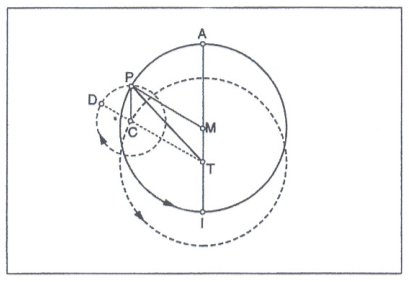
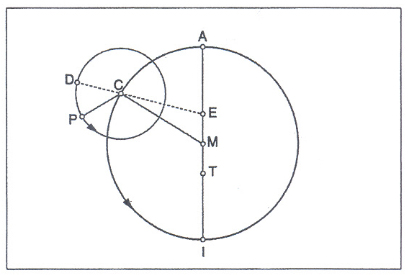
Astronomo, matematico e geografo (n. 100 d. C. circa - m. dopo il 170), vissuto ad Alessandria. Della sua vita conosciamo soltanto quello che si può ricavare dalle sue opere. La sua opera principale è il trattato Μαϑηματικὴ σύνταξις, noto abitualmente con il nome di Almagesto (v.), nel quale T. dà i mezzi matematici di calcolo necessarî alle osservazioni celesti ed espone le teorie astronomiche del tempo, basandosi principalmente sulle osservazioni di Ipparco. Il trattato si compone di tredici libri (principî e trigonometria sferica, sfera celeste, moti del Sole, moti della Luna, distanza Sole-Terra-Luna, eclissi, catalogo di stelle, Via Lattea, teoria dei pianeti). Nel primo libro è contenuto il teorema di Tolomeo (v. oltre). Assunto fondamentale del sistema astronomico tolemaico è che la Terra, di forma sferica, resti immobile al centro della sfera delle stelle fisse. A sostegno di questa ipotesi, T. pone i moti osservabili dei pianeti allora conosciuti (Luna, Mercurio, Venere, Sole, Marte, Giove, Saturno), che descrive mediante modelli cinematici basati su combinazioni di moti circolari uniformi. Sulla base di questi moti T. costruisce tavole accurate delle posizioni dei pianeti in funzione del tempo. Le difficoltà maggiori nella compilazione delle tavole erano rappresentate dalle irregolarità che si osservano nei fenomeni celesti, in particolare nei moti planetarî. Nel fronteggiare tali difficoltà, T. è erede di una tradizione scientifica che risaliva al 4° sec. a. C., in particolare a Eudosso di Cnido e a Platone, e che considerava le irregolarità come l'effetto apparente di una complessità regolata: i moti visibili dei pianeti vi erano intesi come risultanti da composizioni di più moti, ciascuno circolare e uniforme; si trattava perciò di trovare quelle composizioni che generassero per ciascun pianeta il suo moto osservabile. In particolare T. si valse di una specifica famiglia di modelli, chiamata dei deferenti ed epicicli e degli eccentrici, dalle denominazioni dei diversi cerchi con cui erano costruiti. Si consideri anzitutto il Sole, il pianeta più "facile" dato che presenta una sola irregolarità nell'ineguaglianza stagionale, dovuta ai diversi tempi richiesti dal Sole per passare da un punto solstiziale a un punto equinoziale. Nella fig. 1 il piano del foglio è il piano dell'eclittica; T è la Terra, punto di incontro dei due diametri dell'eclittica parzialmente tracciati. Il cerchio API, detto eccentrico in quanto il suo centro M non coincide con quello della Terra, è il percorso del Sole P: si vede immediatamente che P, in moto uniforme intorno a M, visto da T sembra invece variare la propria velocità angolare, ciò che spiega l'ineguaglianza stagionale; si vede anche che il punto di massima velocità angolare è I, il perigeo, quello di minima è A, l'apogeo; il centro dell'eccentrico, dunque, si trova sulla linea che va dalla Terra all'apogeo. Si considerino ora le linee tratteggiate: il cerchio su cui è C, concentrico alla Terra, è il deferente; C, ruota a velocità uniforme ed è a sua volta il centro dell'epiciclo, su cui sono D e P, che ruota uniformemente in senso inverso. Si vede che se l'epiciclo ruota a una velocità tale che CP si mantiene parallelo a TM, e se CP=TM e MP=TC, il modello deferente-epiciclo produce per P lo stesso moto apparente dell'eccentrico: i due modelli dunque sono in questo caso equivalenti. I moti degli altri pianeti sono molto più complessi perché presentano altre irregolarità, la più vistosa delle quali è la frequente occorrenza di moti retrogradi. Qui il modello richiesto è quello deferente-epiciclo. Nella fig. 1 si considerino solo le linee tratteggiate e si inverta la freccia dell'epiciclo in modo che esso ruoti nello stesso senso del deferente: nella fase in cui il pianeta P percorre l'arco di epiciclo più vicino a T e per una velocità sufficientemente grande dell'epiciclo, l'osservatore in T vedrà P compiere sullo sfondo stellare uno spostamento angolare opposto a quello medio. Questa famiglia di modelli cinematici era già stata studiata dal matematico Apollonio di Perga (intorno al 200 a. C.) e impiegata da Ipparco di Nicea (nella seconda metà del 2° sec. a. C.) ma la loro elaborazione estesa a tutti i pianeti, e la conseguente costruzione di tavole, fu opera di Tolomeo. In particolare, poiché il semplice modello deferente-epiciclo non è sufficiente per descrivere i moti retrogradi dei pianeti, perché può generare soltanto archi di retrogradazione (costanti contrariamente a ciò che si osserva), T. costruì modelli combinati a deferente eccentrico (v. la fig. 2, dove T è la Terra, M il centro dell'eccentrico, C quello dell'epiciclo) introducendo in essi ulteriori elementi che li rendevano ancora più complessi. Tra questi il più significativo è l'equante, termine con cui fu in seguito designato il punto E nella fig. 2, simmetrico alla Terra rispetto al centro dell'eccentrico: il centro dell'epiciclo, C, ruota attorno a M come suo centro, ma la sua velocità angolare è uniforme rispetto al punto E. L'introduzione dell'equante è notevole perché con essa T. lascia cadere l'antico principio dell'uniformità dei moti (infatti la velocità lineare di C cessa di essere costante). Nelle ῾Ιποϑέσεις τῶν πλανωμένωγ ("Ipotesi sui pianeti", in due libri) T. dà una versione fisica dei risultati matematici dell'Almagesto e, pur discostandosi in taluni punti dalla cosmologia aristotelica (per es., nella determinazione della causa del movimento delle sfere), ne dipende in gran parte, soprattutto mantenendo la divisione tra sfera celeste e sfera sublunare e assegnando alla sfera celeste una composizione non elementare, ma eterea. Questa costruzione sarà alla base del cosiddetto sistema tolemaico e, variamente combinandosi con la cosmologia aristotelica, dell'immagine del mondo dominante a partire dal sec. 13° fino all'età moderna. Opere minori di astronomia e matematica sono: Περὶ ἀναλήμματος ("Analemma"), sull'orologio solare; Πρόχειροι κανόνες ("Tavole astronomiche manuali"); Φάσεις ἀπλανῶν ἀστέρων καὶ συναγωγὴ ἐπι σημασιῶυ ("Fasi delle stelle fisse e raccolte dei loro dati"), un calendario meteorologico; ῎Απλωσις ἐπιϕανείας σϕαίρας ("Planisforio"), in cui tratta della proiezione stereografica della sfera. Un altro contributo di T. di grande rilievo riguarda la ᾿Οπτικὴ πραγματεία ("Ottica") originariamente in cinque libri, della quale conserviamo la traduzione latina di una traduzione araba degli ultimi quattro (l'ultimo è monco). In essa T. aderisce, come già Euclide, alla scuola pitagorica dei raggi visuali uscenti dall'occhio dove sostituisce tuttavia al "cono prospettico", una piramide con il vertice dell'occhio stesso e la base sul contorno dell'oggetto. In questo modo l'occhio percepisce, attraverso la direzione e la lunghezza dei raggi visuali, la posizione, la forma, la grandezza e il movimento degli oggetti. Nell'Ottica sono trattati i problemi della luce e del colore nella visione, le illusioni ottiche, la riflessione e la rifrazione. Caratteristici di quest'opera, e originali rispetto alla tradizione, sono la considerazione combinata degli aspetti fisici, geometrici e fisiologici della visione e soprattutto il ricorso a esperimenti. Di particolare importanza sono, al riguardo, i risultati sperimentali trovati da T. sul rapporto tra gli angoli di incidenza e di rifrazione e sull'angolo limite nel caso del passaggio della luce da un mezzo più denso a uno meno denso. Nel Medioevo e nel Rinascimento l'ottica tolemaica avrà un'influenza significativa, mediata da importanti modificazioni apportatele dagli arabi. T. scrisse inoltre un compendio di astrologia in quattro libri, il Tetràbiblos. Le influenze celesti sulle vicende terrestri vi sono pensate in termini fisici: le configurazioni celesti, date le proprietà naturali degli astri, sarebbero principî causali di processi che avvengono tra noi. Nell'astrologia di T. gli eventi individuali sono principalmente, ma non completamente, determinati dalla causazione celeste; resta agli uomini un certo margine di intervento. Il Tetràbiblos manterrà nel mondo arabo e in quello europeo fino al Rinascimento una autorità grandissima, anche se non incontrastata. Nel campo della geografia ricordiamo la Γεωγραϕικὴ ὑϕήγησις ("Introduzione geografica"), in otto libri (fondamenti e distinzione tra geografia e corografia, misure della Terra, elenchi di località, confini di paesi, nomi di popoli, divisione dei climi, durata dei giorni, ecc.), in cui T. forniva le istruzioni per la costruzione della mappa del mondo conosciuto. Gli ultimi sette libri contengono essenzialmente l'elenco di più di 8000 località, con le loro coordinate di longitudine e latitudine; il primo istruisce su come tracciare una mappa soddisfacente. Il problema matematico è qui dato dalla sfericità della superficie terrestre, che si tratta di proiettare in piano. T. propone due sistemi alternativi di proiezione, in entrambi i quali inserisce dei termini correttivi, allo scopo di soddisfare l'esigenza che la mappa appaia come la rappresentazione di un globo. L'Introduzione geografica non ebbe seguaci nell'antichità; solo nel 15° sec. fu conosciuta in Occidente. È discussa la questione se l'opera originale fosse corredata da carte o se queste siano state aggiunte posteriormente. Infine, T. redasse un trattato di teoria musicale (῾Αρμονικά "Armonici", in tre libri) che verte sugli intervalli matematici tra note e sul modo di classificarli, basandosi sul comportamento di una corda tesa. Anche in quest'opera è presente lo sforzo di combinare una teoria matematicamente soddisfacente con i fenomeni percettivi. La teoria musicale di T. fu ampiamente usata da Boezio, e per questa via ebbe una certa influenza nei secoli successivi. Molte altre sue opere sono andate perdute. Per il sistema astronomico di T., v. anche solare: Sistema solare. ▭ Teorema di Tolomeo: in un quadrangolo inscritto in una circonferenza, la somma dei rettangoli dei lati opposti è equivalente al rettangolo delle diagonali. Cioè se A, B, C, D sono quattro punti che si succedono su una circonferenza, è: AB•CD+BC•DA=AC•BD.