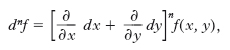potenza
Biologia
In embriologia sperimentale, p. indica il divenire di una parte dell’uovo o dell’embrione, inteso come ‘possibilità’ anziché come ‘capacità’ o ‘potere’. Si distingue dalla competenza (➔) in quanto la p. di una parte caratterizza l’intero periodo dello sviluppo embrionale, compreso quello che precede ogni traccia di competenza.
Fisica e tecnica
Il lavoro di una forza, o di un sistema di forze, riferito all’unità di tempo; in generale, l’energia (meccanica, elettrica, termica ecc.) che in un dato fenomeno viene scambiata nell’unità di tempo.
Caratteri generali
La p. media di una forza F in un intervallo di tempo (t, t+Δt) è il rapporto tra il lavoro compiuto da F nell’intervallo di tempo considerato e l’ampiezza Δt dell’intervallo medesimo. La p. (istantanea) all’istante t è il rapporto tra il lavoro elementare dL, compiuto dalla forza in un tempuscolo dt successivo all’istante t, e il tempuscolo medesimo; come tale, essa si esprime mediante il prodotto scalare F•v della forza all’istante t per la velocità v che al medesimo istante compete al punto cui è applicata la forza. In un caso come nell’altro, la p. misura quindi il valore medio, oppure istantaneo, del lavoro (➔) che la forza compie, o compirebbe, nell’unità di tempo. Immediata è l’estensione a un sistema di forze, per il quale la p. è la somma delle p. delle singole forze; in particolare, per una coppia agente su un corpo in rotazione, la p. è il prodotto scalare del momento della coppia per la velocità angolare del corpo.
Unità di misura della p. nel sistema internazionale di unità di misura (SI) è il watt (simbolo W), p. di un sistema che produce il lavoro di un joule in un secondo (1 W=1 J/s). Nel sistema CGS, unità di misura della p. è l’erg/s (1 erg/s=10–7 W). Nel sistema pratico, per misurare la p., oltre al kgm/s (pari a 9,81 W), è stato spesso usato il cavallo-vapore (simbolo CV) pari a 75 kgm/s e quindi a 735,5 W.
Potenza in impianti o macchine
Il termine p. è di uso corrente nel linguaggio tecnico con riferimento a macchine nelle quali si abbiano comunque trasformazioni di energia. In tal caso generalmente è accompagnato da una particolare specificazione.
Potenza di un autoveicolo
Locuzione generica per indicare la p. resa dal motore di un autoveicolo, misurata al banco di prova, con vari criteri (p. SAE, p. DIN ecc.) oppure con un freno dinamometrico applicato alle ruote motrici (p. alle ruote); è diversa dalla p. fiscale, valutata convenzionalmente per scopi fiscali (➔ automobile).
Potenza continua
In contrapposto a p. di picco e simili, è la p. che una macchina può erogare con continuità per periodi di tempo relativamente lunghi.
Potenza indicata
Per una macchina alternativa, la p. quale risulta dal diagramma fornito da un indicatore di pressione. P. installata Per un impianto, è la p. complessiva dei motori primi dell’impianto.
Potenza motrice
Per una macchina azionata da un motore, la p. occorrente alla macchina per funzionare e che il motore le fornisce.
Potenza nominale
Per una macchina è il valore della p. per il quale sono valide alcune garanzie di funzionamento.
Potenza perduta
Genericamente, è la p. che in una macchina è dissipata a causa di resistenze passive.
Potenza di picco (o di spunto)
P. che una macchina può erogare per brevi periodi di tempo.
Potenza specifica
Per un motore, il rapporto tra la p. resa e la massa; anche, per i motori volumetrici a combustione interna, il rapporto tra la p. resa e la cilindrata. In aeronautica, si distinguono varie p. caratteristiche del propulsore, in relazione alle varie condizioni di volo: p. di decollo, p. normale (cioè erogata per lunghi intervalli di tempo), al suolo, in quota (si specifica a quali quote), per salita, per crociera ecc.
Potenza acustica
Nella propagazione di onde sonore in un mezzo, per il generico punto P del mezzo e un elemento di superficie dS per esso, è il prodotto della pressione acustica agente su dS per l’area di dS e per la componente normale a dS della velocità istantanea delle particelle del mezzo.
Potenza di una corrente fluida
In corrispondenza a una sezione S della corrente fluida è data: a) nel caso di un fluido incompressibile, con buona approssimazione, da
dove ρ è la densità del fluido, v la sua velocità media, p la sua pressione, g l’accelerazione di gravità, z la quota della sezione; b) nel caso di un fluido compressibile da
dove h è l’entalpia specifica del fluido.
Potenza elettrica
Con riferimento a un conduttore percorso da una corrente elettrica di intensità costante i, fra i capi del quale sia mantenuta una tensione costante V, si chiama p. (della corrente nel conduttore) il prodotto, Vi, della tensione per l’intensità di corrente. Se tensione e corrente sono variabili nel tempo e sono V il valore all’istante t della tensione esistente ai capi di un elemento di circuito e i il simultaneo valore dell’intensità di corrente, il prodotto Vi è la p. all’istante t, o p. istantanea, nell’elemento considerato; ha il nome di p. media in un certo intervallo di tempo Δt il valore medio della p. istantanea in tale intervallo:
Le precedenti definizioni si estendono all’intero circuito della corrente, a patto di sostituire alla tensione V la forza elettromotrice agente nel circuito. Se la corrente è periodica, la p. media è generalmente riferita all’intervallo di un periodo ed è detta anche p. attiva. Per una corrente sinusoidale la p. attiva è uguale al prodotto dei valori efficaci della tensione e dell’intensità di corrente per il coseno dello sfasamento ϕ tra corrente e tensione, mentre ha il nome di p. reattiva il prodotto dei valori efficaci anzidetti per il seno di ϕ, e quello di p. apparente il prodotto dei soli valori efficaci; il rapporto tra la p. attiva e la p. apparente, pari, per quanto ora detto, a cosϕ, ha il nome di fattore di potenza. Naturalmente la p. effettivamente utilizzabile è la p. attiva; quella reattiva è una p. puramente convenzionale che si considera quando si vuole esprimere la quota parte della p. apparente non utilizzabile in conseguenza dello sfasamento fra corrente e tensione. Come unità di misura si usa per la p. media il watt (simbolo W), e il suo multiplo, il kilowatt (1 kW=1000 W); nel caso di corrente sinusoidale la p. attiva è misurata in watt, la p. apparente in voltampere (simbolo VA) e la reattiva in voltampere reattivi (simbolo VAR oppure var).
La potenza in ottica
In ottica, la p. di una lente o di un sistema ottico è, qualitativamente parlando, la maggiore o minore capacità della lente o del sistema di adempiere al suo scopo e, quantitativamente parlando, lo stesso di convergenza (o potere diottrico); p. luminosa equivale a flusso luminoso.
Matematica
Prodotto di più fattori uguali
La p. di un numero reale è il prodotto di più fattori uguali a quel numero, che si dice base della p., mentre il numero dei fattori uguali si chiama esponente. Per es.: 5∙5∙5 = 125 (p. di base 5 ed esponente 3); in simboli: 53, leggi: «5 alla terza p.», o semplicemente «5 alla terza». Più in generale, per la p. di base a ed esponente n, si scrive: an, e si legge: «a all’ennesima p.», «a alla p. n» o «a elevato a n». Alcune proprietà fondamentali delle p. sono: 1) am∙an = am+n; 2) se m>n, am/an = am–n; 3) (am)n = amn. Il concetto di p. può essere esteso anche ai casi in cui l’esponente è nullo, negativo, frazionario, reale qualsiasi, o anche complesso, purché si conservino le proprietà sopra enunciate. Possiamo infine notare che se a>0 e γ è reale, la p. aγ è sempre reale e positiva. Se 0< a <1 essa tende a +∞ quando γ tende a –∞ ed è infinitesima al tendere di γ a ∞; se a>1, i due limiti si invertono. Viceversa, se a<0 e γ = m/n è un numero razionale irriducibile, la p. risulta reale solo se n è dispari (in particolare, se n = 1 ossia se γ è intero); se n è pari oppure se γ è reale, il valore della p. è un numero complesso.
Potenza a esponente zero
Se si estende la seconda proprietà anche al caso in cui m = n, si ha: am/an = 1 = am–n = a0, e quindi la p. a esponente zero di un numero si assume uguale all’unità.
Potenza a esponente negativo
Se la stessa proprietà si vuole estendere al caso in cui n>m (n–m = t>0) si ha: am/an = 1/an–m = am–n, cioè se t>0, si pone a–t = 1/at.
Potenza a esponente razionale (frazionario)
Giacché, per definizione di radice n-esima, è (n√‾‾‾am)n=am, per conservare la terza proprietà (e insieme le altre), bisognerà porre (am/n=n√‾‾‾am). Si osservi che la base a può essere anche un numero negativo, tranne il caso in cui l’esponente sia m/n con n pari e m dispari. In tal caso il simbolo am/n va evitato, in quanto non ha senso (nel campo reale) il radicale di indice pari di un numero negativo. Se n è pari e am>0, il radicale (n√‾‾‾am)=am/n ha due determinazioni, l’una positiva, l’altra negativa; per evitare ambiguità, si usa attribuire allora al simbolo am/n il valore positivo (aritmetico) di detto radicale. Sono possibili due inversioni dell’operazione di elevazione a p.: la prima si ottiene quando si considerano noti la p. a e l’esponente n, e si considera incognita la base b (estrazione della radice n-esima di a); la seconda, quando si considerano note la base b e la p. a, e incognito l’esponente n (ricerca del logaritmo di a in base b).
Potenza a esponente reale
È la p. aγ, ove γ è un numero reale; si definisce considerando una successione di numeri razionali c1, c2, …, cn, … che abbia come limite γ e costruendo la successione delle p ac1, ac2, …, acn: si dimostra che tale successione è convergente e il suo limite è la p. aγ.
Potenza a esponente complesso
È la p. ab, con a, b entrambi complessi (a≠o); si definisce ponendo ab = exp(b loga) e riconducendosi quindi all’esponenziale e al logaritmo nel campo complesso. Questa definizione dà luogo però, in generale, a infiniti valori per ab, giacché nel campo complesso il logaritmo è una funzione a infiniti valori. Per es., ii = exp(i log i) = exp[–(π/2+2kπ)]; le infinite determinazioni della p. corrispondono ai diversi valori interi di k.
Potenza di un punto rispetto a una circonferenza
Se da un punto P del piano di una circonferenza C si conduce una retta che la incontri in due punti A e B, il prodotto delle lunghezze dei due segmenti PA e PB si mantiene costante al variare della secante per P. Questo prodotto, preso positivamente o negativamente a seconda che P sia esterno o interno a C, si dice p. del punto P rispetto alla circonferenza. Inoltre, se P è esterno alla circonferenza, la sua p. è uguale al quadrato di uno dei due segmenti PT, PT′ tangenti alla circonferenza e uscenti da P.
Potenza (o infinità) di un insieme
È il numero cardinale degli elementi dell’insieme; tale numero può essere finito o comunque transfinito (➔ cardinale; transfinito); nel caso di un insieme finito, la sua p. è nient’altro che il numero dei suoi elementi. In generale, si dice che due insiemi hanno la stessa p. o sono equipotenti, se esiste una corrispondenza biunivoca tra i loro elementi. Si dice che un insieme A ha p. maggiore di un insieme B se A non è equipotente a B ma esiste in A un sottoinsieme equipotente a B.
Insieme potenza di un insieme
Sia A un qualsiasi insieme (finito o infinito); si indica con ℬ (A) (leggi: «P gotico di A») e si chiama insieme p. di A l’insieme che ha come elementi tutti i sottoinsiemi di A.
Potenza simbolica
Un operatore che debba applicarsi a una o più funzioni si può talora esprimere sotto forma di p. simbolica di un binomio o polinomio contenente funzioni o simboli di significato diverso da un caso all’altro. Eseguita la p. secondo le regole formali dell’algebra, le p. e i prodotti dei simboli dovranno poi interpretarsi in senso operatorio. Per es., l’espressione del differenziale n-esimo dnf di una funzione f(x,y) di due variabili si può scrivere come p. n-esima simbolica:
pur d’intendere le p. e i prodotti dei due simboli di derivazone ∂/∂x, ∂/∂y come simboli di derivazioni n-esime da applicare alla funzione f(x,y).
Storia
A Firenze, nei sec. 14°-17°, si chiamavano p. certe compagnie popolari che avevano come compito principale di fare pubblici festeggiamenti.