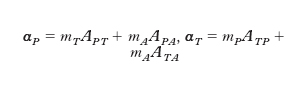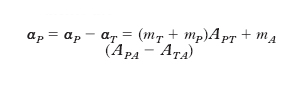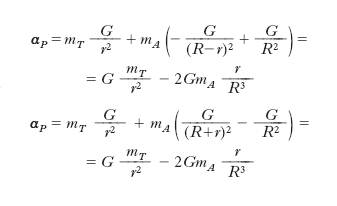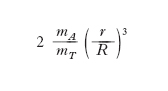marea
Fenomeno consistente in periodiche oscillazioni del livello marino di differente ampiezza e fase, connesse a fattori astronomici, ma fortemente influenzate dalla forma e dalla topografia sia dei bacini oceanici sia delle coste. La fase corrispondente alla massima elevazione del livello marino si chiama alta m., quella corrispondente al massimo abbassamento bassa m.; la fase di aumento del livello è il flusso, l’altra è il riflusso. La differenza di livello tra alta e bassa m., l’ampiezza della m., varia considerevolmente da luogo a luogo. In generale essa è piccola nei mari interni; in oceano aperto è piuttosto irrilevante, mentre viene esaltata lungo le aree costiere o nei bacini marini di forma particolare per effetto dei fenomeni di risonanza.
In sedimentologia prendono il nome di sedimenti di m. o tidali i sedimenti deposti negli ambienti dominati dalle azioni delle maree.
Teoria delle maree
Teoria statica delle maree. - La prima teoria delle m., la cosiddetta ‘teoria statica’, basata solo sugli effetti gravitazionali, fu elaborata da D. Bernoulli, C. MacLaurin, L. Euler circa un cinquantennio dopo la formulazione della legge di Newton della gravitazione universale. In questa teoria si schematizza la Terra, un generico astro e una masserella di acqua posta in un punto della superficie terrestre con tre punti materiali T, A, P rispettivamente di massa mT, mA, mP; in un sistema di riferimento inerziale le accelerazioni αP di P e αT di T, per la seconda legge della dinamica, sono date da
avendo indicato con AIJ l’azione gravitazionale che l’unità di massa di J esercita sull’unità di massa di I (ovviamente AIJ = −AJI). L’accelerazione di P relativa a T (o, più precisamente, rispetto a un sistema di riferimento solidale con T i cui assi hanno direzioni invariabili rispetto al riferimento inerziale) è data da
.
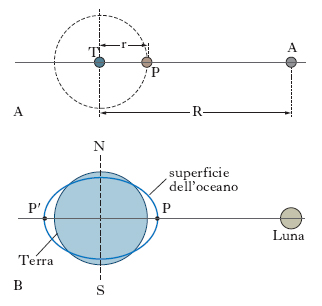
Calcolando questa accelerazione nelle posizioni della masserella d’acqua indicate in fig. 1 A, essendo trascurabile mP rispetto a mT e nell’ipotesi che la distanza R Terra-astro sia molto maggiore del raggio r della Terra (R≫r), si ottiene
dove G è la costante di gravitazione universale. Pertanto una massa unitaria di acqua del mare posta sulla congiungente del centro della Terra e di un astro, sia in congiunzione con l’astro (in P) sia in opposizione (in P′), subisce l’azione (la cosiddetta forza di m.) di modulo F=2 GmA r/R3 di pari intensità nei due siti, contraria all’attrazione terrestre, di modulo GmT/r2, cioè diretta lungo la verticale locale dal basso in alto. Importante per valutare la forza di m. è il suo rapporto con l’attrazione terrestre:
,
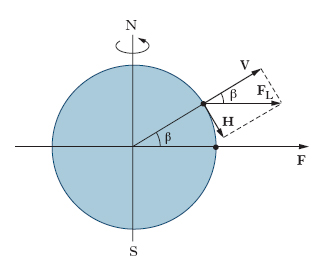
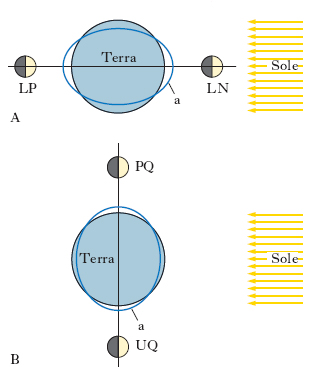
il quale, nel caso che l’astro perturbatore sia la Luna vale, 1,1∙10−7, nel caso sia il Sole 0,5∙10−7. La forza di m. della Luna è quindi 2,2 volte quella del Sole. Solo la Luna (per la sua vicinanza alla Terra) e il Sole (per la sua grande massa) producono effetti di m. apprezzabili. Considerando il caso ideale di un globo terrestre interamente ricoperto dal mare, sotto l’azione della Luna la superficie libera delle acque verrebbe ad assumere la forma di un ellissoide di rotazione con asse maggiore coincidente con la congiungente i centri della Terra e della Luna (fig. 1B). La forza di m. ha infatti valore massimo lungo la congiungente Terra-Luna e diminuisce al crescere della latitudine; in un punto qualsiasi sarà FL=F∙cosβ (fig. 2); il vettore FL può inoltre essere scomposto in una componente verticale (V), che non ha alcun effetto sulle acque, e in una componente orizzontale (H), chiamata anche forza attratti;va, che determina le m.: H=F∙sen β∙cos β. La forza di m. è massima alle sizigie (Luna nuova LN, Luna piena LP, fig. 3A), quando Terra, Luna e Sole si trovano allineati e la m. lunare si somma a quella solare; è minima alle quadrature (primo quarto PQ, ultimo quarto UQ, fig. 3B). L’ellissoide di m. a compie un intero giro in un giorno lunare (24 ore e 50 minuti), cosicché, considerando un punto qualunque P della superficie terrestre, per esso passano successivamente i due massimi e i due minimi dell’ellissoide stesso: se ne conclude che la m. ha un periodo semidiurno esattamente la metà del giorno lunare (12h 25m), che da un giorno all’altro la m. ritarda di 50m e che, nel corso del mese lunare, i massimi di alta m. (grandi m.) coincidono con le sizigie e i minimi (piccole m.) con le quadrature; la differenza di altezza fra grandi e piccole m. è detta differenza semimensile. In realtà però i moti di m. risultano ben più complicati e la teoria statica da sola non è sufficiente a spiegare la dinamica delle maree.
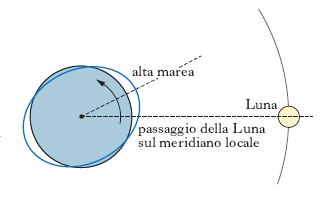
Teoria dinamica delle maree. - Tiene conto sia dell’inerzia delle masse d’acqua sia degli effetti della rotazione terrestre, fu sviluppata da P.-S. Laplace all’inizio dell’Ottocento e perfezionata successivamente. In merito quindi alla periodicità e alla ampiezza di m. venne così messo in evidenza il ruolo che svolgevano l’inclinazione dell’asse terrestre, le variazioni delle distanze Terra-Luna e Terra-Sole legate all’eccentricità delle orbite, nonché il fatto che il piano orbitale lunare è inclinato di 5° rispetto a quello dell’eclittica e ruota lentamente con un periodo di 18,6 anni. Inoltre, tenuto conto che la Terra non è uniformemente ricoperta da una unica massa d’acqua, venne evidenziato il ruolo che svolge la geografia, con la diversa distribuzione delle masse continentali, nonché la forma dei diversi bacini oceanici; questi ultimi infatti hanno un proprio periodo di oscillazione che è in relazione con la profondità, con la morfologia del fondale, con le loro dimensioni e con la forma delle coste, che può dar luogo a fenomeni di risonanza meccanica che amplificano l’ampiezza di m. grazie all’azione periodica delle forze di marea. Un ruolo non trascurabile svolge anche la forza di Coriolis, legata alla rotazione terrestre. Anche l’attrito gioca un ruolo importante poiché mentre la Terra ruota al di sotto dei due rigonfiamenti, essa trascina l’onda di m., determinando così un ritardo di alcune ore tra il passaggio della Luna al meridiano locale e il verificarsi dell’alta o della bassa m. (ora del porto) il quale è costante per un determinato punto della costa (fig. 4).
Tutti i fattori citati hanno in sostanza messo in evidenza la complessità della teoria dinamica delle m. che si può così riassumere: in un particolare sito la m. è la risultante (m. globale) della sovrapposizione di più m. parziali, il cui periodo è legato ai moti della Luna e del Sole ma la cui ampiezza e la cui fase variano con le condizioni locali. Riguardo al periodo le m. si dividono in tre classi: m. semidiurne, nelle quali si hanno due alte e due basse m. in un giorno lunare; m. diurne, con una sola alta e bassa m. in un giorno lunare; m. miste, che sono le più frequenti e sono costituite dalla sovrapposizione di una m. diurna e una semidiurna, con la conseguenza che uno dei due massimi della m. semidiurna è maggiore dell’altro (per mezzo mese è più alta l’alta m. del mattino, e per il mezzo mese successivo è più alta l’alta m. del pomeriggio: la differenza tra le due altezze si chiama differenza giornaliera di m.). Particolare importanza hanno le sovramaree, caratterizzate dal fatto di avere un periodo multiplo di quello delle m. parziali componenti.
È da osservare infine che il regime di m. è notevolmente influenzato dalle condizioni meteorologiche locali, particolarmente dalle variazioni di pressione atmosferica e dal vento, che eccitano nei bacini acquei ristretti onde stazionarie note col nome di sesse. Le oscillazioni delle sesse vanno a sovrapporsi a quelle di m., e, se il periodo delle due è poco diverso, possono verificarsi, specie in concomitanza con altre condizioni meteorologiche, eccezionali alte e basse maree.
Correnti di marea
I moti di m. generano correnti che consistono nello scorrimento orizzontale di masse d’acqua che hanno sempre la caratteristica di essere semidiurne, diurne e miste. Tali correnti, di lieve entità in pieno oceano, assumono viceversa forme imponenti quando vengono a muoversi alternativamente in canali, stretti ed estuari dove possono raggiungere velocità superiori a 1 m/s. Queste correnti di m. (onde di m. fluviale) risultano dalla composizione di due distinti moti cui sono soggette le acque del fiume, e cioè quello dell’onda di traslazione provocata nel fiume dal dislivello di m. alla foce e quello della corrente di ritorno che a essa inevitabilmente si accompagna. Infatti, l’onda di traslazione diminuisce di volume nel risalire il corso del fiume a causa della resistenza opposta dall’alveo: la massa d’acqua che essa via via abbandona, rifluendo alla foce, viene appunto a formare la corrente di ritorno. La velocità dell’onda di traslazione ha, in una certa sezione del fiume, un andamento in accordo con le fasi della m. alla foce; l’andamento della velocità della corrente di ritorno, largamente influenzato dalle caratteristiche dell’alveo fluviale, risulta invece, in generale, non in fase con la m. stessa. La velocità dell’onda di m. è, istante per istante, la somma algebrica delle due velocità, per cui l’onda stessa è una corrente di flusso (diretta cioè dalla foce a monte) per tutto il tempo in cui la velocità dell’onda di traslazione è, in valore assoluto, maggiore della velocità della corrente di ritorno; è una corrente di riflusso (diretta cioè verso la foce) per il tempo restante; quando le due velocità si equivalgono, non si ha corrente di m. (stanca di alta m., stanca di bassa m.). Le onde di m. fluviale assumono talora forme imponenti, dando luogo al fenomeno del mascheretto, anche denominato della ‘barra di flusso’, influenzando notevolmente il regime della navigazione fluviale.
Osservazione delle maree
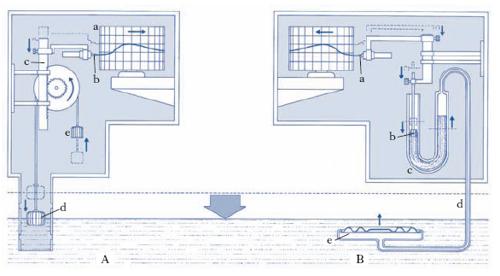
L’osservazione delle m. si effettua con strumenti misuratori del livello marino: il mareometro è sostanzialmente simile agli idrometri e come questi può essere di tipo a galleggiante, a pressione e a ultrasuoni; il mareografo è un mareometro registratore. Il tipo più spesso usato è quello a galleggiante: si tratta di un idrometrografo (apparecchio di misura che serve a determinare la quota del pelo liquido di un corso o specchio d’acqua) costruito in modo tale da poter registrare le massime ampiezze di m. del luogo d’osservazione (fig. 5A). Sono talora usati anche mareografi a pressione, costituiti essenzialmente da una capsula manometrica posta sul fondo marino e collegata a un manografo (fig. 5B); con una opportuna taratura dello strumento si può risalire dalle variazioni di pressione registrate alle corrispondenti variazioni del livello marino. I mareografi a ultrasuoni utilizzano un trasduttore a ultrasuoni in grado di emettere impulsi verso la superficie della quale occorre misurare la distanza e di rivelare gli echi di ritorno; l’elettronica di controllo consente la determinazione e la registrazione della distanza da misurare in base al tempo intercorso fra emissione e ricezione.
Previsione delle maree
Con il progressivo estendersi della rete mareografica a tutto il globo è possibile eseguire previsioni delle m. in un qualsivoglia sito costiero della Terra mediante l’uso dei calcolatori. L’importanza delle m. nei riguardi della navigazione, specialmente per l’accesso ai porti, impone ai naviganti di prevedere o almeno stimare l’ora e l’altezza delle maree. Generalmente le previsioni di m. sono date in modo completo per i porti principali; per quelli secondari, situati entro una certa distanza da quello principale, si fa la stima delle m. in base ad alcuni elementi noti (ritardo e rapporti d’ampiezza rispetto al porto principale). Tuttavia la previsione delle m., fatta utilizzando le tecniche dell’analisi armonica, resta comunque un fatto complicato poiché i fenomeni a esse collegati variano con larghi intervalli di periodicità proprio in ragione dell’interazione tra i movimenti della Luna e del Sole, nonché in ragione della variabilità della topografia sia dei fondali oceanici sia delle coste. Mentre i fenomeni legati alle m. sono stati e sono molto studiati sia nelle regioni costiere, sia sulle piattaforme continentali, sono meno conosciuti per le aree oceaniche. L’utilizzo dei satelliti e della telemetria ha portato a notevoli progressi; con l’uso infatti di particolari tecniche, come per es. l’altimetria con microonde, è stato possibile misurare valori assoluti della posizione del livello marino con una precisione di circa 10 cm (conoscendo i dati del geoide e dell’orbita del satellite).
M. atmosferica
Fenomeno consistente in oscillazioni regolari dell’atmosfera terrestre, provocate sia dall’azione gravitazionale della Luna e del Sole, sia dall’azione termica del Sole. Sulla superficie terrestre tale m. si manifesta con oscillazioni periodiche regolari della pressione atmosferica, aventi ampiezze di circa 1-3 millibar.
M. terrestre
Fenomeno consistente in oscillazioni della crosta solida della Terra, le quali dimostrano che essa non è rigida ma elastica e quindi può deformarsi sotto l’effetto delle stesse forze che producono le altre maree. Le ampiezze delle m. terrestri vengono valutate con metodi gravimetrici; l’azione che esse esercitano è dimostrata dal fatto che l’ampiezza delle m. oceaniche è in realtà solo il 70% dell’ampiezza media teorica; rimane quindi un 30% che viene appunto assorbito dalla Terra grazie al comportamento elastico della crosta e che genera quindi le m. terrestri. Di conseguenza, l’ampiezza delle m. che attualmente noi osserviamo è più piccola di quella che avrebbe avuto la Terra se fosse stata completamente rigida.