distribuzione
Economia
Attività che provvede alla collocazione sul mercato delle merci e dei servizi, e quindi l’insieme dei punti di vendita che ne assicurano agli acquirenti la disponibilità.
Nell’ingegneria gestionale e nel linguaggio dell’organizzazione aziendale, il processo di d. si colloca nell’area dei processi di vendita e ha l’obiettivo di fornire ai diversi canali o direttamente al cliente finale i prodotti che l’azienda realizza. Negli anni più recenti, con la crescita di complessità della catena di approvvigionamento (➔) e con la possibilità che la rete Internet offre di semplificare notevolmente il raggiungimento del cliente, questo processo ha assunto un ruolo fondamentale per l’efficacia delle vendite dell’azienda.
Nel linguaggio economico, si parla di d. del reddito nel senso di ripartizione dello stesso tra i fattori di produzione e di tutti i problemi a essa connessi. Si distingue lo studio della d. funzionale (che si propone di spiegare in quale modo si determinino i compensi di quanti partecipano al processo produttivo) da quello della d. personale (che si propone invece di indagare come i diversi gruppi di redditieri si distribuiscano a seconda della entità del reddito). La concezione iniziale dei classici, collegando la d. del reddito alle classi sociali storicamente rilevanti (proprietari terrieri, salariati, borghesia industriale nascente), configurò la d. come un processo conflittuale tra rendite crescenti, salari reali stazionari e profitti decrescenti. La concezione conflittuale si accentua nella visione marxista, imperniata sul concetto di plusvalore (➔). Con il marginalismo (➔) l’analisi della d. si identifica con il processo di determinazione dei prezzi in condizioni di mercato ipoteticamente concorrenziali. Ciascun fattore, in tal caso, viene remunerato in funzione del contributo dato al processo produttivo e la d. appare sostanzialmente armonica. Si sono anche tuttavia indagate forme di mercato diverse dalla concorrenza pura, quali la concorrenza imperfetta, la concorrenza monopolistica, il monopolio bilaterale. Anche gli sviluppi della teoria keynesiana hanno lasciato la propria traccia nell’evoluzione della teoria della d., collegando la quota del reddito spettante ai salari alle decisioni di investimento degli imprenditori (➔ Kaldor, Nicholas). Più di recente, la d. del reddito è stata considerata (➔ Sraffa, Piero) non come fatto meccanicistico risultante dal processo di formazione dei prezzi, ma come conseguenza di assetti istituzionali dipendenti dalle scelte umane e da esse modificabili; il premio Nobel, Amartya Kumar Sen, ha dato contributi importanti sul legame fra d. dei r. personali, benessere e ineguaglianza.
Informatica
Con il termine d. (ingl. dispatching) si indica una fase del processo di avvicendamento dei vari programmi, in un calcolatore che lavori in multielaborazione.
Matematica
Teoria delle d. La nozione di d., introdotta da L. Schwartz, generalizza la nozione fondamentale di funzione comprendendo, tra l’altro, anche le cosiddette ‘funzioni impulsive’. La teoria delle d. deve il suo interesse anche alla possibilità di introdurre delle operazioni di derivazione e di integrazione indefinita per le d. e trova importanti applicazioni nello studio delle equazioni differenziali. Limitandoci per semplicità al caso di una sola variabile, si consideri una funzione reale ϕ(x) di una variabile reale che sia di classe C∞ (cioè dotata delle derivate di tutti i possibili ordini) e che sia nulla all’infuori di un insieme chiuso e limitato (insieme compatto di punti) dell’asse delle x. La famiglia Φ di tutte le funzioni ϕ(x) del tipo anzidetto costituisce uno spazio vettoriale nel campo reale (spazio base delle d.) nel quale è possibile introdurre una nozione di convergenza, dicendo che una successione di funzioni ϕ1(x), ϕ2(x), ..., ϕn(x), ... (tutte nulle all’infuori di un medesimo insieme compatto) converge alla funzione ϕ(x) quando non soltanto la successione tende uniformemente alla funzione ϕ(x), ma inoltre la successione delle derivate di un qualunque ordine r, cioè
tende anch’essa uniformemente alla
(derivata r-ma della funzione ϕ). Avendo introdotto tale nozione di convergenza nello spazio base Φ, è possibile parlare di ‘continuità’ in Φ stesso. Ciò premesso si intende per d. nello spazio Φ ogni funzionale F(ϕ) definito in Φ, che sia lineare, per il quale cioè
per ogni ϕ1, ϕ2 in Φ e a1, a2 numeri reali, e inoltre sia continuo, cioè risulti
[
]
ogni qualvolta la successione ϕn tenda a ϕ nel senso sopra specificato. Per le d. si può introdurre una operazione di derivazione e una di integrazione in certo senso analoghe a quelle relative alle funzioni ordinarie. Così la derivata n-esima F(n)(ϕ) di una d. F(ϕ) è definita dalla relazione:
dove ϕ(n) è la derivata n-esima della funzione ϕ; essa risulta ancora una distribuzione. Anche l’operazione di integrazione di una d., concepita come inversa della derivazione, ha senso e ha come risultato una distribuzione. L’importanza delle d. risiede, tra l’altro, nel fatto che, data la loro estrema generalità, permettono di inquadrare in una stessa struttura teorie matematiche differenti, e soprattutto di sviluppare una rigorosa teoria analitica per certi enti matematici che, rimanendo fuori del dominio dell’analisi classica, non erano stati inizialmente considerati come enti analitici veri e propri. Esempio tipico in proposito è quello della cosiddetta funzione δ(x) di Dirac, che non è una funzione nel senso ordinario perché, se come tale potesse interpretarsi, essa dovrebbe soddisfare le condizioni:
[
]
ma le sue proprietà possono inquadrarsi nella teoria delle d., consentendo uno sviluppo analitico perfettamente rigoroso del calcolo di Dirac; lo stesso dicasi del calcolo simbolico di Heaviside ecc. La teoria delle d. ha già avuto importanti applicazioni, per es., nella teoria della misura e in topologia algebrica, ma ancor più ha mostrato di essere adeguato strumento di progresso nella teoria delle equazioni differenziali, per opera dello stesso Schwartz e di numerosi altri analisti.
D. di frequenza e d. di probabilità
Sia data una collettività di individui, o un insieme di elementi od oggetti dello stesso tipo, per es. automobili, e si decida di classificare gli elementi stessi basandosi sulle modalità con le quali in essa si manifesta un certo carattere (per es., l’età nel caso degli individui, o la velocità massima nel caso delle automobili). Si ottiene così una d. statistica. Questa può essere di due tipi: di frequenza e di probabilità. Una d. di frequenza consiste nell’indicazione delle frequenze con cui le varie modalità di un carattere compaiono nella totalità dei casi esaminati. Le frequenze possono essere assolute (quando indicano il numero delle volte che la modalità si presenta) o relative (uguali alle frequenze assolute divise per il numero totale dei casi; la somma delle frequenze relative è naturalmente uguale a uno). Una d. di probabilità indica invece le probabilità con cui le varie modalità di un carattere si possono presentare in una prova. Le modalità possono essere qualitative o quantitative; il numero che varia assumendo le diverse modalità (o determinazioni) si chiama variabile statistica nel caso di una d. di frequenza, e variabile casuale o variabile aleatoria nel caso di una d. di probabilità. Le d. di probabilità e le d. di frequenza sono concettualmente diverse, tuttavia se si considerano le frequenze relative lo studio di esse è sostanzialmente lo stesso.
Una d. e la variabile aleatoria a essa legata si dice semplice o a una dimensione se riguarda un solo carattere, multipla o a più dimensioni se riguarda più caratteri (per es., la statura e il peso di un gruppo di persone); si dice poi discreta se presenta solo un numero finito o un’infinità numerabile di modalità; continua se le modalità possono invece variare in modo graduale, continuo. Nella realtà le d. di frequenza sono sempre discrete, perché provengono da un numero finito di casi; esse però sono spesso interpretate, per comodità di studio, come d. continue.
Rappresentazione della funzione di ripartizione di una distribuzione
Una d. si può rappresentare mediante la sua funzione di ripartizione o di d., che, nel caso di una d. semplice, è una funzione F(x) che indica, per ogni valore reale x, la probabilità, o la frequenza, con cui la variabile X assume un valore minore di x; in simboli, per d. di probabilità (il caso delle d. di frequenza è del tutto analogo): F(x) = Pr {X < x}. La funzione di ripartizione è non decrescente, continua a sinistra, e si ha
viceversa ogni funzione soddisfacente a tali condizioni individua una d. della quale essa è la funzione di ripartizione. Una d. si dice assolutamente continua (o, da alcuni, continua) se tale è la funzione di ripartizione;
si dice fun-
zione di densità. Sue proprietà caratteristiche sono:
In corrispondenza a una d. a n dimensioni si ha una variabile casuale (o statistica) n-pla (X1, X2, ..., Xn), di cui le variabili X1, X2, ... si dicono componenti. La funzione di ripartizione è definita allora da
le funzioni di ripartizione F1(x1), F2(x2), ... delle variabili componenti sono dette marginali. Le componenti si dicono indipendenti se
3. Valori medi e momenti di una distribuzione
Sia X una variabile aleatoria, F(x) la sua funzione di ripartizione: si chiama valor medio (o valore atteso) della X, e si indica con E(x), il valore, supposto finito, del-
Il momento
r-esimo, o di ordine r, è definito da μr=E(Xr); i momenti centrali o rispetto alla media μ1 sono dati da [13]
tra questi ha particolare importanza il momento del secondo ordine, chiamato varianza e indicato con σ2x. I momenti fattoriali sono poi definiti da
Per una d. doppia i momenti sono definiti da
e analogamente per d. a più dimensioni. Se X e Y sono indipendenti in senso intuitivo, si ha:
E(XY) = E(X) E(Y);
viceversa, se vale questa relazione, X e Y si dicono incorrelate.
Indici di variabilità e di concentrazione
La varianza di una d. fornisce una misura della variabilità della d. stessa: essa è uguale a zero se e solo se la probabilità (o frequenza) è concentrata in un unico punto, se cioè la variabile è praticamente costante. Esistono però altri indici di variabilità; tra questi è importante la differenza media di C. Gini (➔ differenza); infine, se la variabile X è sempre maggiore di zero, si ha il rapporto di concentrazione d/2μ1 (dove d è la differenza media) che serve a precisare numericamente il concetto intuitivo di concentrazione; applicato, per es., alla d. della ricchezza in un gruppo di persone, vale zero se tutti posseggono la stessa ricchezza, ha il valore massimo se tutto l’ammontare della ricchezza appartiene a una sola persona.
Principali tipi di distribuzione
Una delle d. più importanti è la d. di Bernoulli o d. binomiale che si ottiene nel classico problema delle prove ripetute (➔ anche Bernoulli, Giacomo I). Se si ripete n volte una prova in cui un evento ha in ogni prova la probabilità p di verificarsi e q=1−p di non verificarsi, il numero A di volte che l’evento si verifica è una variabile casuale che assume i valori 0, 1, ..., n con probabilità pi=(ni)piqn−i (i = 0,1,…,n). Tale d. ha media np e varianza npq. È anche molto importante nelle applicazioni la d. di Poisson o dei piccoli numeri, secondo la quale la probabilità che una variabile casuale as;suma i valori 0, 1, 2, ... è e−m mi/i! (i=0, 1, 2, ...), dove m è un parametro reale positivo. Essa si ottiene dalla d. di Bernoulli, ponendo p=m/n e facendo tendere n all’infinito. Tale d. ha media m e varianza m. Dalla d. di Bernoulli si ottiene anche, come limite, la d. normale o di Gauss, che è una d. continua con funzione di densità:
Essa rappresenta, con buona approssimazione, l’andamento di molti fenomeni; ciò perché, sotto condizioni molto ampie, la somma di n variabili casuali tende, per n molto grande, ad avere d. normale (➔ convergenza). La d. uniforme su un intervallo (a, b), o d. rettangolare, ha funzione di densità f(x) = 1/(b-a) per a<x<b, nulla altrove. La d. di tipo gamma ha, per ν>0, λ>0, funzione di densità uguale a 0 per x≤0 e a [λ/Γ(ν)](λx)ν−1e−λx per x>0, dove Γ è la funzione gamma (➔ gamma): la sua media è ν/λ, la sua varianza ν/λ2. Per ν=1 si ha la d. esponenziale (negativa); per ν=g/2 e λ=1/2 si ha la d. a indice chi quadro o d. chi quadro (➔ chi); il parametro g, intero positivo, è detto numero dei gradi di libertà. La d. di tipo beta ha per r>0, s>0, funzione di densità f(x)=xr−1(1−x)s−1/B(r, s) per 0<x<1, nulla altrove, dove B è la funzione beta (➔ beta). La d. di Cauchy ha, per λ>0, funzione di densità [λ2+(x-μ)2]λ/π.
TECNICA
D. dell’acqua potabile
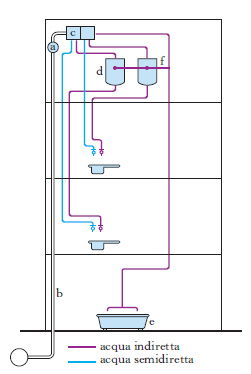
La rete di d. è il complesso delle tubazioni che dal serbatoio di un acquedotto si diramano nelle varie direzioni raggiungendo tutti i punti di utilizzazione (➔ acquedotto e condotta). La d. dell’acqua all’interno degli edifici può essere fatta con due sistemi diversi, a bocca tassata (od orifizio tassato) e a contatore. Col primo sistema, sulla colonna montante, o subito prima degli apparecchi di utilizzazione, è disposto un apparecchio (lente idrometrica) che limita la portata lasciando passare con continuità una quantità d’acqua costante, mentre l’acqua non consumata viene accumulata in serbatoi posti sulla sommità dell’edificio; col secondo sistema si può prelevare dalla condotta di alimentazione una portata qualunque (compatibilmente con la capacità delle tubazioni), misurata mediante l’impiego di una serie di contatori, uno per ciascun appartamento, posti tra la colonna montante e gli apparecchi di utilizzazione. Il sistema a contatore è preferibile dal punto di vista igienico, perché elimina le possibilità di inquinamento dell’acqua nei serbatoi; tuttavia richiede una disponibilità d’acqua notevole nei periodi di punta del consumo.
Il sistema a bocca tassata può a sua volta essere a d. diretta o a d. indiretta (fig. 1); nel primo sistema si hanno tanti sbocchi quanti sono gli utenti e l’acqua passa direttamente dalla conduttura nel serbatoio corrispondente, mentre con il secondo, più usato, esiste una sola lente idrometrica a sulla colonna montante b, da dove l’acqua passa nella cassetta distributrice c, che la ripartisce distribuendola nei serbatoi d dei diversi utenti e ai servizi comuni (lavatoi e), ai quali viene inoltre addotta l’acqua proveniente dal tubo f del troppopieno dei cassoni; con quest’ultimo sistema è possibile avere anche la cosiddetta acqua semidiretta: la cassetta di d. provvede in tal caso a inviare parte dell’acqua proveniente dalla colonna montante direttamente nella colonna discendente ai vari utenti, mentre la rimanente è distribuita ai serbatoi.
D. del gas di città
Se il gas viene ottenuto in appositi stabilimenti (officine del gas) per distillazione dei carboni o per conversione ossidante di idrocarburi (➔ gas), la d. si effettua attraverso condotte principali (alimentatrici), che si diramano dai gasometri delle officine, e ramificazioni secondarie fino ai singoli edifici; lo schema generale della rete di d. è analogo a quello impiegato negli acquedotti e può essere a ramificazione o a stella (numerosi collettori che si dipartono dall’officina sui quali si innestano le ramificazioni) oppure a maglia o ad anello (un grande collettore periferico chiuso, dal quale vengono derivati tutti gli altri tronchi). Nei casi in cui i luoghi di utilizzazione non sono molto distanti da quello di produzione, a vincere le perdite di carico dovute al moto del gas nelle tubazioni può bastare la pressione prodotta dalle campane gasometriche e il dislivello eventualmente esistente tra quelle e la zona di erogazione (se questa si trova a quota più elevata, la pressione atmosferica ivi regnante è inferiore e perciò facilita l’afflusso del gas). Altrimenti, si ricorre a compressori: nelle condotte principali, interrate, d’acciaio, con giunti a saldatura autogena fasciati con iuta catramata, è immesso il gas a valori della pressione da qualche decimo di bar fino ad alcuni bar. Ai punti terminali vi sono gasometri compensatori oppure apparecchi che riducono e regolano automaticamente la pressione in modo da adeguarla alle variazioni del consumo. Da essi si dirama la rete per la d. a bassa pressione, formata da tubi di ghisa interrati, collegati da giunti a bicchiere sigillati con stoppa catramata e piombo colato. Questi tubi sono posati con leggera pendenza e nei punti di quota minima sono installati dei sifoni ove si raccoglie periodicamente l’acqua di condensazione. Nel caso di metanizzazione, cioè di impiego diretto di gas naturale nella stessa rete utilizzata in precedenza per la d. del gas di città tradizionale (cioè ottenuto nelle officine del gas), occorre evitare le perdite di gas per effetto dell’essiccamento delle guarnizioni impiegate nelle giunzioni delle vecchie tubazioni; a tale scopo si umidifica il gas naturale o si provvede ad apposita impermeabilizzazione delle tubazioni; è opportuno, inoltre, odorizzare il gas naturale.
D. nelle macchine a fluido
Nelle macchine motrici a fluido, termiche o idrauliche, il termine d. indica sia l’operazione sia l’insieme di organi meccanici mediante i quali il fluido motore è messo a contatto, periodicamente o con continuità, con gli organi della macchina ai quali deve cedere, secondo il ciclo di funzionamento, una parte della propria energia; nelle macchine alternative la d. provvede anche a espellere il fluido che ha lavorato. Quando la d. si effettua mediante organi mobili, si utilizzano valvole, cassetti, foderi, dischi, saracinesche, rubinetti, ugelli con spina ecc., azionati automaticamente dalla stessa macchina, talvolta soggetti all’azione di un regolatore (a comando meccanico, idraulico, elettrico, pneumatico).
D. nei motori a combustione interna
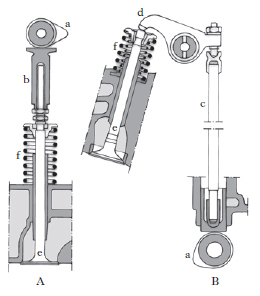
È di regola ottenuta, nei motori alternativi a quattro tempi, mediante valvole separate per l’introduzione e per lo scarico, comandate da camme calettate su un albero (albero della d.) mosso dall’albero motore tramite ingranaggi, catene o cinghie dentate (fig. 2). Le camme (a) agiscono sulle valvole direttamente oppure per il tramite di punterie (b; fig. 2A) o di meccanismi composti da aste (c; fig. 2B) e bilancieri (d), e comandano le valvole e nel senso dell’apertura delle luci, mentre apposite molle di richiamo (f) consentono alle valvole di ritornare in posizione di chiusura; solo nel caso di motori molto veloci si ricorre talvolta al comando desmodromico (➔) delle valvole, che agisce sia nella corsa di apertura sia in quella di chiusura. Nei motori per autoveicoli e per motoveicoli, la d. con valvole laterali richiede un tempo più lungo per il riempimento e lo scarico del cilindro e per la combustione della carica; la d. con valvole in testa, invece, consente una forma più raccolta e regolare (emisferica) della camera di combustione e una migliore disposizione delle candele, così da ottenere, con una combustione più rapida e più completa, una maggior velocità del motore e un minor consumo specifico. È comune a tutti i motori la d. incrociata, che consiste nell’anticipare l’apertura e ritardare la chiusura delle valvole: l’apertura delle valvole di aspirazione avviene prima del punto morto superiore di aspirazione e la chiusura di quelle di scarico dopo il punto morto superiore di scarico. Inoltre le valvole di aspirazione si chiudono con ritardo e quelle di scarico si aprono con anticipo. In tal modo sono favoriti sia l’afflusso della colonna di gas freschi dai condotti d’ammissione sia lo scarico dei gas combusti, e nel breve intervallo in cui le valvole sono contemporaneamente aperte si inserisce una fase di lavaggio della camera di combustione. Nei motori a due tempi, la d. può essere fatta dallo stantuffo stesso che, nel suo movimento, scopre e ricopre delle luci praticate sulla parete del cilindro, aventi posizione e sagoma tali da consentire una buona realizzazione delle fasi del ciclo.

![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/c/cf/FORMULE_distribuzione_01.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/0/0f/FORMULE_distribuzione_02.jpg)
![[3]](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f5/FORMULE_distribuzione_03.jpg)
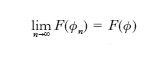
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/50/FORMULE_distribuzione_05.jpg)
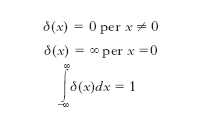
![[7]](https://images.treccani.it/ext-tool/intra/thumbs_medium/0/0b/FORMULE_distribuzione_07.jpg)
![[8]](https://images.treccani.it/ext-tool/intra/thumbs_medium/b/b2/FORMULE_distribuzione_08.jpg)
![[9]](https://images.treccani.it/ext-tool/intra/thumbs_medium/d/dd/FORMULE_distribuzione_09.jpg)
![[10]](https://images.treccani.it/ext-tool/intra/thumbs_medium/3/3f/FORMULE_distribuzione_10.jpg)
![[11]](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/99/FORMULE_distribuzione_11.jpg)
![[12]](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/91/FORMULE_distribuzione_12.jpg)
![[13]](https://images.treccani.it/ext-tool/intra/thumbs_medium/1/1f/FORMULE_distribuzione_13.jpg)
![[14]](https://images.treccani.it/ext-tool/intra/thumbs_medium/4/4e/FORMULE_distribuzione_14.jpg)
![[15]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/56/FORMULE_distribuzione_15.jpg)
![[16]](https://images.treccani.it/ext-tool/intra/thumbs_medium/8/8d/FORMULE_distribuzione_16.jpg)